[이론 스터디] 벡터와 행렬 기본 개념 :: DATA 분석 & 엔지니어링 스터디 기록 공간 (tistory.com)
[이론 스터디] 벡터와 행렬 기본 개념
벡터(vector)의 정의 1) 숫자를 원소로 가지는 리스트 또는 배열 #리스트 x = [1,2,3] #배열 x = np.array([1,2,3]) 행 벡터: 열 벡터: 2) 공간에서의 한 점 3) 원점으로부터 상대적 위치 0~1 사이의 값을 곱..
lime-juice.tistory.com
백터 기본 개념은 위 포스트를 참고
Norm
- 원점에서부터의 벡터의 거리
- L1, L2 두가지 방식으로 계산 가능
- norm의 종류에 따라 기하학적 성질이 달라진다. (L1과 L2에 따라 거리의 정의가 다르기 때문)

L1 (맨하탄 거리):
- 벡터의 각 성분의 변화량의 절대값(absolute value)를 모두 더하여 거리 계산
- 예를 들어 a = [2,3]인 2차원 벡터가 있다고 가정한다면, 빨간 선이 a의 norm이다.
- ((2,3)에 위치한 벡터의 원점에서부터 맨하탄 거리는 5가 될 것이다.

L2 (유클리드 거리):
- 벡터의 각 성분의 변화량의 제곱의 합에 루트를 씌워 계산한다.
- 똑같이 a = [2,3]인 2차원 벡터가 있다고 가정한다면, 빨간 선이 a의 norm이다.
- 피타고라스 정리를 사용하여 유클리드 거리를 계산할 수 있으며, ((2,3)에 위치한 벡터의 원점에서부터 유클리드 거리는 루트 13이 될 것이다.
두 벡터 사이의 거리
- L1, L2 norm으로 계산 가능
- 벡터의 뺄셈을 이용
- 그림에서처럼 2차원 공간에서는 보라색 선이 두 백터 사이의 거리가 된다.

두 백터 사이의 각도
- L2 norm으로만 계산 가능
- 제 2 코사인 법칙을 이용
- 두 벡터의 내적을 두 벡터의 L2 곱으로 나누어 thea의 코사인 값을 계산한다.
- 코사인의 역함수(아크코사인)을 계산하면 두 벡터 사이의 각도인 theta를 구할 수 있다.
정사영(orthogonal projection)
- 수직으로 빛을 비추어 투영되는 부분을 뜻한다.
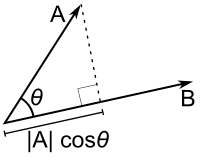
- 벡터 a의 길이( |a| )에 theta의 코사인 값(cos theta)을 곱하면 a의 정사영된 길이(Proj(a))를 계산할 수 있다.
- 벡터 b의 길이만큼 a의 정사영 길이를 조정한 값이 내적이다. (스칼라 곱 <- 벡터 길이 조정)
- 두 벡터의 유사도를 측정하는 데에 사용이 가능하다.
'AI 배경지식' 카테고리의 다른 글
| Transformer와 Autoregressive 생성 모델 (0) | 2025.04.06 |
|---|---|
| Receptive Field 설명 (CNN vs Transformer) (0) | 2022.09.20 |
| 벡터와 행렬 기본 개념 (0) | 2021.08.19 |



