벡터(vector)의 정의
1) 숫자를 원소로 가지는 리스트 또는 배열
#리스트
x = [1,2,3]
#배열
x = np.array([1,2,3])행 벡터:
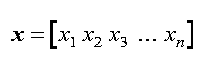
열 벡터:

2) 공간에서의 한 점
3) 원점으로부터 상대적 위치

0~1 사이의 값을 곱하면 방향은 그대로이고 길이만 변하며, 음수를 곱할 경우 반대 방향이 된다. (스칼라곱 = 각각의 구성 성분에 스칼라를 곱하는 것, 길이가 변하게 됨)
행렬(matrix)의 정의
1) 벡터를 원소로 가지는 2차원 배열
X = np.array([[1,2,3],
[4,5,6],
[7,8,9]])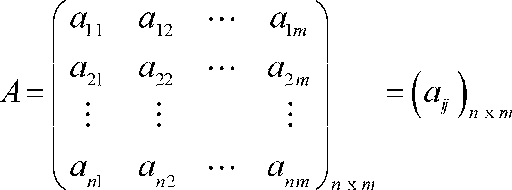
2) 공간에서의 여러 점들 (데이터의 모임)
3) 벡터 공간에서 사용되는 연산자 (다른 데이터를 연결) -> 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다. (행렬 곱셈 부분 참고)
덧셈/뺄셈
같은 모양을 가지면 계산 가능
벡터:
- 벡터는 원점으로부터 상대저 위치를 표현. 벡터의 덧셈/뺄셈은 다른 벡터로부터 상대적 위치이동을 표현

행렬:
성분곱(Hadamard product)
- 같은 모양을 가지면 계산 가능
벡터:

행렬:
내적 (inner product)
벡터:
- 두 벡터의 성분곱의 합
- 두 벡터의 유사도 측정에 사용
행렬:
- i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산
- X의 행(m)의 개수와 Y의 행(m)의 개수가 같아야 한다.
- numpy: inner(X, Y)
행렬 곱셈
- i 번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산
- X의 열(n)의 개수와 Y의 행(m)의 개수가 같아야 한다.
- numpy: X @ Y
- n x m 크기의 행렬에 m크기의 벡터를 곱할 경우 n크기의 벡터를 계산할 수 있다.
- m은 곧 차원을 의미함으로 벡터를 m차원의 공간에서 n차원의 공간에 보낸다고 표현할 수 있다.
- 위 행렬곱에서 단지 p가 1로 바뀌었을 뿐이다.
- 행렬곱을 통해 패턴을 추출하거나 데이터를 압축할 수 있다.
- 모든 선형변환은 행렬곱으로 계산할 수 있다.
역행렬
- 어떤 행렬의 연산을 거꾸로 되돌리는 행렬
- 1) 행(m)과 열(n)의 크기가 같고 2)행렬식(determinant)이 0이 아닌 경우에만 계산이 가능

- 그림의 예시에서 A의 크기는 2 x 2, A의 역행렬의 크기도 2 x 2로 동일
- numpy: np.linalg.inv( X )
- A 행렬과 A 역행렬을 곱할 경우 항등행렬이 계산된다.

- identity matrix(항등행렬, I) = 대각원소들이 1이면 나머지 원소들은 0인 정방행렬, 임의의 행렬 A를 항등행렬에 곱할 경우 output으로 A 행렬이 그대로 나온다.
- 넘파이로 계산할 경우 그림에서 보듯히 정확이 0은 아니지만 0에 매우 가까운 값이 표기될 수도 있다.
'AI 배경지식' 카테고리의 다른 글
| Transformer와 Autoregressive 생성 모델 (0) | 2025.04.06 |
|---|---|
| Receptive Field 설명 (CNN vs Transformer) (0) | 2022.09.20 |
| 벡터 사이의 거리, 각도 계산 (0) | 2021.08.19 |



